Volume Formulas
Note: "ab" means "a" multiplied by "b". "a2" means "a squared", which is the same as "a" times "a". "b3" means "b cubed", which is the same as "b" times "b" times "b".
Be careful!! Units count. Use the same units for all measurements. Examples
cube = a 3 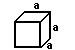
rectangular prism = a b c 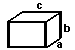
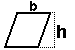
irregular prism = b h 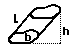
cylinder = b h = pi r 2 h 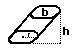
pyramid = (1/3) b h 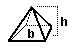
cone = (1/3) b h = 1/3 pi r 2 h 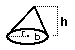
sphere = (4/3) pi r 3 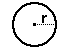
ellipsoid = (4/3) pi r1 r2 r3 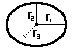
  Units Units
Volume is measured in "cubic" units. The volume of a figure is the number of cubes required to fill it completely, like blocks in a box.
Volume of a cube = side times side times side. Since each side of a square is the same, it can simply be the length of one side cubed.
If a square has one side of 4 inches, the volume would be 4 inches times 4 inches times 4 inches, or 64 cubic inches. (Cubic inches can also be written in3.)
Be sure to use the same units for all measurements. You cannot multiply feet times inches times yards, it doesn't make a perfectly cubed measurement.
The volume of a rectangular prism is the length on the side times the width times the height. If the width is 4 inches, the length is 1 foot and the height is 3 feet, what is the volume?
NOT CORRECT .... 4 times 1 times 3 = 12
CORRECT.... 4 inches is the same as 1/3 feet. Volume is 1/3 feet times 1 foot times 3 feet = 1 cubic foot (or 1 cu. ft., or 1 ft3). |
| |
|
Surface Area Formulas
In general, the surface area is the sum of all the areas of all the shapes that cover the surface of the object.
Note: "ab" means "a" multiplied by "b". "a2" means "a squared", which is the same as "a" times "a".
Be careful!! Units count. Use the same units for all measurements. Examples
| Surface Area of a Cube = 6 a 2 |
 (a is the length of the side of each edge of the cube) (a is the length of the side of each edge of the cube)
In words, the surface area of a cube is the area of the six squares that cover it. The area of one of them is a*a, or a 2 . Since these are all the same, you can multiply one of them by six, so the surface area of a cube is 6 times one of the sides squared.
| Surface Area of a Rectangular Prism = 2ab + 2bc + 2ac |
 (a, b, and c are the lengths of the 3 sides) (a, b, and c are the lengths of the 3 sides)
In words, the surface area of a rectangular prism is the area of the six rectangles that cover it. But we don't have to figure out all six because we know that the top and bottom are the same, the front and back are the same, and the left and right sides are the same.
The area of the top and bottom (side lengths a and c) = a*c. Since there are two of them, you get 2ac. The front and back have side lengths of b and c. The area of one of them is b*c, and there are two of them, so the surface area of those two is 2bc. The left and right side have side lengths of a and b, so the surface area of one of them is a*b. Again, there are two of them, so their combined surface area is 2ab.
| Surface Area of Any Prism |
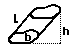 (b is the shape of the ends) (b is the shape of the ends)
Surface Area = Lateral area + Area of two ends
(Lateral area) = (perimeter of shape b) * L
Surface Area = (perimeter of shape b) * L+ 2*(Area of shape b)
| Surface Area of a Sphere = 4 pi r 2 |
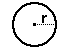 (r is radius of circle) (r is radius of circle)
| Surface Area of a Cylinder = 2 pi r 2 + 2 pi r h |
 (h is the height of the cylinder, r is the radius of the top) (h is the height of the cylinder, r is the radius of the top)
Surface Area = Areas of top and bottom +Area of the side
Surface Area = 2(Area of top) + (perimeter of top)* height
Surface Area = 2(pi r 2) + (2 pi r)* h
In words, the easiest way is to think of a can. The surface area is the areas of all the parts needed to cover the can. That's the top, the bottom, and the paper label that wraps around the middle.
You can find the area of the top (or the bottom). That's the formula for area of a circle (pi r2). Since there is both a top and a bottom, that gets multiplied by two.
The side is like the label of the can. If you peel it off and lay it flat it will be a rectangle. The area of a rectangle is the product of the two sides. One side is the height of the can, the other side is the perimeter of the circle, since the label wraps once around the can. So the area of the rectangle is (2 pi r)* h.
Add those two parts together and you have the formula for the surface area of a cylinder.
Surface Area = 2(pi r 2) + (2 pi r)* h
a circle
|
| Definition: A circle is the locus of all points equidistant from a central point. |
Definitions Related to Circles
arc: a curved line that is part of the circumference of a circle
chord: a line segment within a circle that touches 2 points on the circle.
circumference: the distance around the circle.
diameter: the longest distance from one end of a circle to the other.
origin: the center of the circle
pi ( ): A number, 3.141592..., equal to (the circumference) / (the diameter) of any circle. ): A number, 3.141592..., equal to (the circumference) / (the diameter) of any circle.
radius: distance from center of circle to any point on it.
sector: is like a slice of pie (a circle wedge).
tangent of circle: a line perpendicular to the radius that touches ONLY one point on the circle. |
Diameter = 2 x radius of circleCircumference of Circle = PI x diameter = 2 PI x radius
where PI =  = 3.141592... = 3.141592...
Area of Circle:
area = PI r2 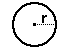
Length of a Circular Arc: (with central angle  ) )
if the angle  is in degrees, then length = is in degrees, then length =  x (PI/180) x r x (PI/180) x r
if the angle  is in radians, then length = r x is in radians, then length = r x 
Area of Circle Sector: (with central angle  ) )
if the angle  is in degrees, then area = ( is in degrees, then area = ( /360)x PI r2 /360)x PI r2
if the angle  is in radians, then area = (( is in radians, then area = (( /(2PI))x PI r2 /(2PI))x PI r2
Equation of Circle: (Cartesian coordinates)
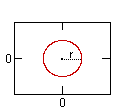
for a circle with center (j, k) and radius (r):
(x-j)^2 + (y-k)^2 = r^2
Equation of Circle: (polar coordinates)
for a circle with center (0, 0): r( ) = radius ) = radius
for a circle with center with polar coordinates: (c,  ) and radius a: ) and radius a:
r2 - 2cr cos( - -  ) + c2 = a2 ) + c2 = a2
Equation of a Circle: (parametric coordinates)
for a circle with origin (j, k) and radius r:
x(t) = r cos(t) + j y(t) = r sin(t) + k
 | | |
Perimeter Formulas
The perimeter of any polygon is the sum of the lengths of all the sides.
Note: "ab" means "a" multiplied by "b". "a2" means "a squared", which is the same as "a" times "a".
Be careful!! Units count. Use the same units for all measurements. Examples
square = 4a 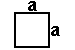
rectangle = 2a + 2b 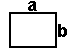
triangle = a + b + c 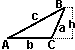
circle = 2pi r 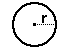
circle = pi d (where d is the diameter)
The perimeter of a circle is more commonly known as the circumference.
 |
| | |
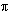 = 3.141592...)
= 3.141592...)

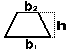
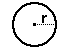
 [s(s-a)(s-b)(s-c)] when s = (a+b+c)/2 (Heron's formula)
[s(s-a)(s-b)(s-c)] when s = (a+b+c)/2 (Heron's formula)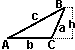
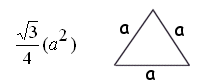


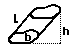

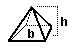

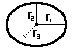
 (h is the height of the cylinder, r is the radius of the top)
(h is the height of the cylinder, r is the radius of the top) ): A number, 3.141592..., equal to (the circumference) / (the diameter) of any circle.
): A number, 3.141592..., equal to (the circumference) / (the diameter) of any circle. )
)
 ) and radius a:
) and radius a:
No comments:
Post a Comment